小学生の頃、算数の先生に「定規を使わずに紙を3等分に折る方法を知っているか」と問われ、方法も考え方も教えてもらわないまま卒業してしまった。
成人してからそのことをふと思い出し、じっくり考えた結果、答えが出た。
以下、方法を解説するので自力で考えたい人はスクロール注意です。
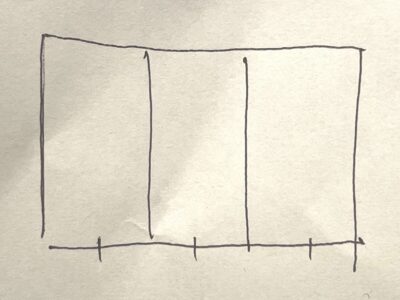
そもそも紙を3等分に折るとは、こういう状態を作るということです。

答えを求めるまでには、補助線を作るために3回折る必要がある。
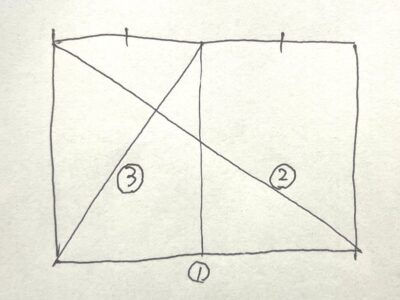
①紙を横半分に折る
②紙を斜め半分に折る
③ ②の折り目とクロスするように、ある角から対辺の半分の点(①で作った折り目)までを結ぶ線に沿って折る
こうすると、②と③の線で交点ができる。
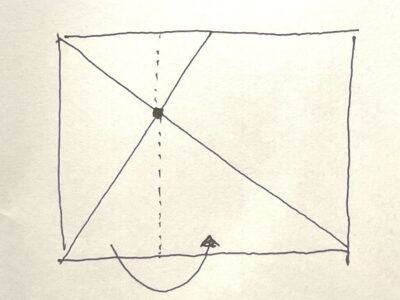
この交点を通るように一辺をまっすぐ折ると……
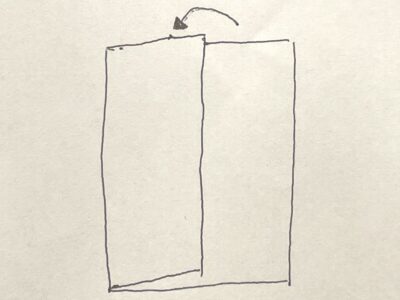
ちょうど3等分になるように折れるのだ。
納得するためには各自実際に紙を折ってみるのがいいと思う。
私は理屈ではなく、紙をあれこれ折っているうちにこの答えにたどり着いた。
しかし必ず理屈があるはずだからと追って考えたら、一つ納得できる説明が作れた。
そして、それが他者によってどう解説されているか答え合わせをするためにネットを検索してみたところ、私がまったく思いつけなかった説明が出てきた。というか複数サイトを見てもそれが一般的なようで、私が考えたやり方には出会うことができなかった。
そこで、今回はそのよく見る説明を紹介したのち、私の考えた説明も添えようと思う。
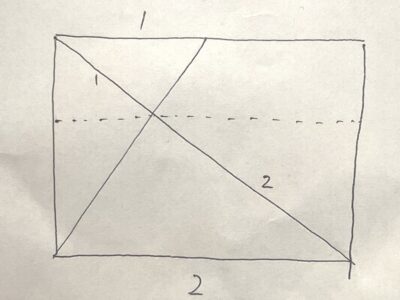
一般的な解説は、「折り目の中に相似の三角形を見る」というものだった。
斜めになった砂時計のような2つの三角形がある。これが相似(角がすべて等しく、各辺の比が等しい状態)になっている。
上の三角形の底辺は下の三角形の底辺の半分だから、ほかの辺の長さも1:2になっている。
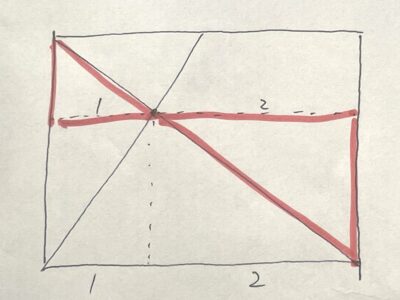
「2つの折り目の交点を通り、かつ紙の一辺に平行」な線を引いて作られる2つの三角形(図中の赤)もそれぞれ相似だから、交点は紙の各辺を1:2に分ける(=3等分する)ということになる。
これがネットで見つけた解説だった。
以下は、私の考え方。

紙をこういうグラフと見る。2つの折り線をそれぞれ一次関数と捉える。

紙の辺の長さをa、bとする。

短い方の線は、x軸の増加量=a/2、y軸の増加量=b。
長い方の線は、x軸の増加量=a、y軸の増加量=-b、切片=b。
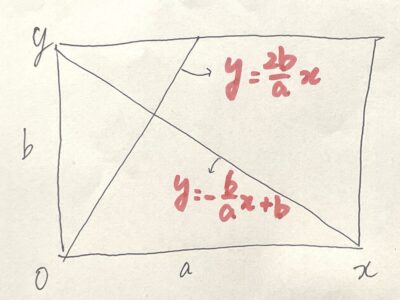
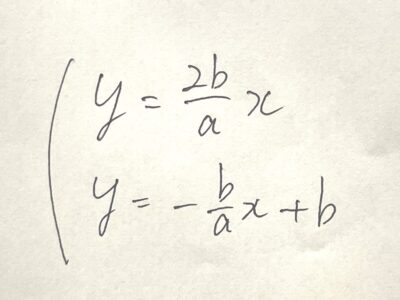
これらの交点の座標を求める。
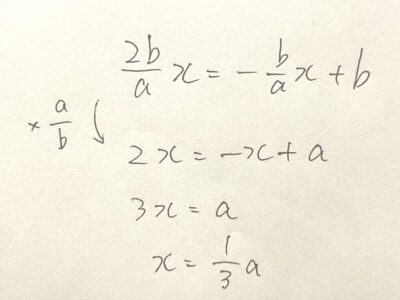
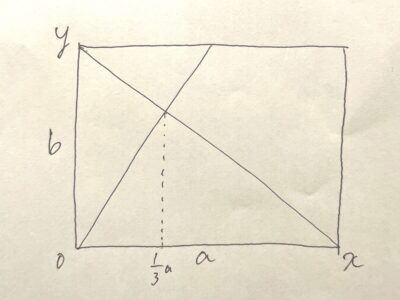
計算すると、交点のx座標はこのようになり、長辺aを1:2に分けるポイントであることが分かる。
という考え方をしました。
もし同じ考え方で答えにたどり着いた人の参考になればいいなと思って書いた。
あとは当時の算数の先生に教えてやりたい。解けましたよー。
